Fuerza sobre una carga en movimiento.

Investiguemos los efectos de un campo magnético observando la fuerza magnética ejercida
sobre una carga que pasa a través del campo. Para estudiar estos efectos, es útil imaginar un
tubo de iones positivos como el de la figura 29.13. Dicho tubo nos permite inyectar un ion
positivo de carga y velocidad constantes en un campo de densidad de flujo magnético B.
Orientando el tubo en varias direcciones, podemos observar la fuerza ejercida sobre la carga
en movimiento. La observación más importante es que dicha carga experimenta una fuerza
que es perpendicular tanto a la densidad de flujo magnético B, como a la velocidad v de la
carga en movimiento. Observe que cuando el flujo magnético se dirige de izquierda a derecha
y la carga se mueve hacia donde está el lector, la carga se desvía hacia arriba. Si se invierte la
polaridad de los imanes, se provoca que la carga se desvíe hacia abajo.
La dirección de la fuerza magnética F sobre una carga positiva en movimiento con una
velocidad v en un campo de densidad de flujo B, puede considerarse mediante la regla del
tornillo de rosca derecha (véase la figura 29.14):



Investiguemos los efectos de un campo magnético observando la fuerza magnética ejercida
sobre una carga que pasa a través del campo. Para estudiar estos efectos, es útil imaginar un
tubo de iones positivos como el de la figura 29.13. Dicho tubo nos permite inyectar un ion
positivo de carga y velocidad constantes en un campo de densidad de flujo magnético B.
Orientando el tubo en varias direcciones, podemos observar la fuerza ejercida sobre la carga
en movimiento. La observación más importante es que dicha carga experimenta una fuerza
que es perpendicular tanto a la densidad de flujo magnético B, como a la velocidad v de la
carga en movimiento. Observe que cuando el flujo magnético se dirige de izquierda a derecha
y la carga se mueve hacia donde está el lector, la carga se desvía hacia arriba. Si se invierte la
polaridad de los imanes, se provoca que la carga se desvíe hacia abajo.
La dirección de la fuerza magnética F sobre una carga positiva en movimiento con una
velocidad v en un campo de densidad de flujo B, puede considerarse mediante la regla del
tornillo de rosca derecha (véase la figura 29.14):

La regla de la mano derecha: Extienda la mano derecha con los dedos apuntando
en la dirección del campo B y el pulgar apuntando en la dirección de
la velocidad v de la carga en movimiento. La palma abierta está de cara a la
fuerza magnética F sobre una carga positiva.
Si la carga en movimiento es negativa, la dirección de la fuerza se determina siguiendo el
mismo procedimiento pero usando la mano izquierda. De esta manera la dirección de la fuerza
magnética es opuesta a la dirección para una carga positiva.
Consideremos ahora la magnitud de la fuerza sobre una carga en movimiento. La experimentación
ha mostrado que la magnitud de la fuerza magnética es directamente proporcional
a la magnitud de la carga q y a su velocidad v. El tubo de ion positivo indicará, por medio de
mayores desviaciones, si alguno de estos parámetros aumenta.
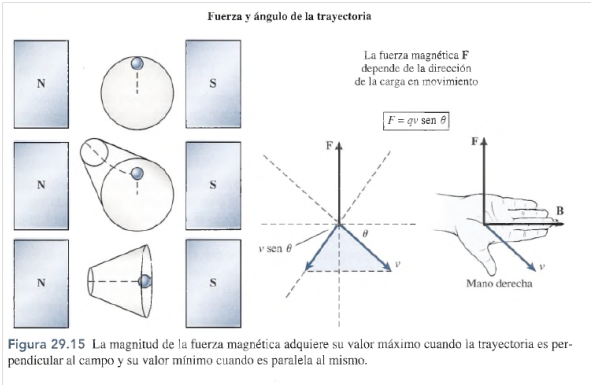
Se observará una variación no esperada en la fuerza magnética si el tubo del ion se hace
girar lentamente respecto a la densidad de flujo magnético B. Como indica la figura 29.15,
para una carga dada con velocidad constante v, la magnitud de la fuerza varía con el ángulo

que forma el tubo con el campo. La desviación de la partícula es máxima cuando la velocidad
de la carga es perpendicular al campo. Cuando el tubo se hace girar lentamente hacia B, la
desviación de la partícula disminuye gradualmente. Por último, cuando la velocidad de la carga
tiene una dirección paralela a B, no ocurre ninguna desviación, lo que indica que la fuerza
magnética ha caído hasta cero. Claramente la magnitud de la fuerza es función no sólo de la
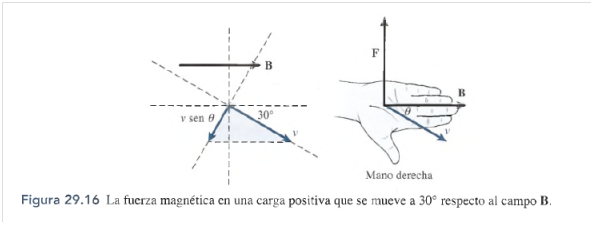
magnitud de la carga y de su velocidad, sino que también varía con el ángulo 6 entre v y B. Esta
variación se explica al establecer que la fuerza magnética es proporcional a la componente de
la velocidad, v sen 6, perpendicular a la dirección del campo. (Consulte la figura 29.16.)
Las observaciones anteriores se resumen por la proporcionalidad
F oc qv sen 8 (29.7)
Si se eligen las unidades apropiadas, la constante de proporcionalidad puede igualarse con la
densidad de flujo magnético B del campo causante de la fuerza. En realidad, esta proporcionalidad
se usa a menudo para definir la densidad de flujo magnético como una razón constante:
B =
F
qv sen 9
(29.8)
Un campo magnético que tenga una densidad de flujo equivalente a 1 tesla
(1 weber por metro cuadrado), ejercerá una fuerza igual a 1 newton sobre una
carga de 1 coulomb que se mueva en forma perpendicular al campo, con
una velocidad de 1 metro por segundo.
Como consecuencia de la ecuación (29.8), se observa que
1 T = 1N/(C • m/s) = 1 N/A • m (29.9)
Estas relaciones entre unidades son útiles para resolver problemas que incluyan fuerzas magnéticas.
Despejando la fuerza F en la ecuación (29.8), obtenemos
F = qvB sen 6 (29.10)
que es la forma más útil para calcular directamente las fuerzas magnéticas. La fuerza F está
en newtons cuando la carga q se expresa en coulombs, la velocidad v se mide en metros por
segundo y la densidad de flujo B se expresa en teslas. El ángulo 6 indica la dirección de v
respecto a B. La fuerza F siempre es perpendicular tanto a v como a B. La dirección de estos
vectores puede determinarse por medio de la aplicación de la regla de la mano derecha.
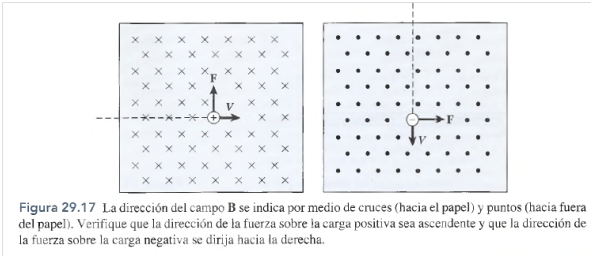
Cuando se representan vectores tridimensionales gráficamente, resulta útil la convención de
utilizar cruces (X) para indicar una dirección hacia el papel. Estos símbolos podrían considerarse
el “inicio” de las flechas de vector. Usaremos puntos ( • ) para indicar puntas de flecha de vector
que apuntan hacia fuera del papel. En la figura 29.17 se muestran dos ejemplos de este tipo. Para
probar su comprensión del tema, verifique que la fuerza sobre la carga positiva es ascendente y
la que la fuerza en la carga negativa se dirige hacia la derecha.

Ejemplo 29.2 T Un electrón se proyecta de izquierda a derecha en un campo magnético dirigido verticalmente
hacia abajo. La velocidad del electrón es de 2 X 106 m/s, y la densidad de flujo magnético
del campo es 0.3 T. Determine la magnitud y la dirección de la fuerza magnética
ejercida sobre el electrón.
Pía n: La carga del electrón es 1.6 X 10 19 C, la magnitud de la fuerza sobre el electrón se
calcula a partir de la ecuación (29.10) y la dirección se determina al aplicar la regla de la
mano izquierda. Se usa la mano izquierda porque la carga de un electrón es negativa.
Solución: El electrón se mueve en una dirección perpendicular a B. Por tanto, sen 0 =1 ;
resolvemos para la fuerza en la siguiente forma:
F = qvB sen 90° = (1.6 X 10~19C)(2 X 106 m/s)(0.3 T)(l)
F = 9.60 X 10~14N
La aplicación de la regla de la mano izquierda para un electrón muestra que la dirección de
la fuerza es hacia afuera de la página, o hacia el lector. (Para una carga positiva como un
protón o una partícula alfa, sería hacia adentro de la página.)